Venturo dichas

¿Qué letra va en cada casilla coloreada? Explíquese.

Recorrido ido ido ido

En las nueve casillas en blanco coloque los números del 1 al 9 de forma que al realizar el recorrido señalado cada vez que pasamos de una casilla a la siguiente en horizontal (tanto a la izquierda como a la derecha) le sumamos una cantidad X y cada vez que nos desplazamos en vertical (tanto hacia arriba como hacia abajo) le restamos una cantidad Y.

Repartir

1 - 0
2 - 0, 5
3 - 0, 3, 6
4 - 0, 2, 4, 7
5 - 0, 2, 4, 6, 8
6 - 0, 1, 3, 5, 6, 8
7 - 0, 1, 2, 4, 5, 7, 8
8 - 0, 1, 2, 3, 5, 6, 7, 8
9 - 0, 1, 2, 3, 4, 5, 6, 7, 8

¿Qué? ¿este es difícil?,
naaaaaa,  quiero decir : no
Si sabes que pregunto sabes la solución.

Teclado numérico

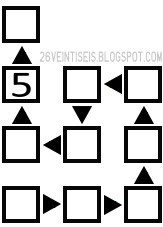
El otro día le presté a un amigo el teclado numérico recién estrenado que tengo para el ordenador portátil.

Lo necesitaba porque le habían hecho responsable de introducir todos los datos del marcador de un torneo deportivo.

Terminado el torneo me lo devolvió así:

¿De qué deporte era el torneo?

¿Par o impar?

En el bombo están 9 bolas con los números del 1 al 9

Se sacarán dos bolas.

Para ganar el premio le piden que acierte si el producto de los dos números extraídos será par o impar.

¿usted que elige?

¿qué probabilidad de acierto tiene?

Era fácil ¿verdad?

Ahora nos proponen que si bien seguimos teniendo que acertar si será par o impar el producto de los dos números, podemos elegir entre tres alternativas:

1 -Que solo sea válido cuando el resultado del producto sea un número de una sola cifra. (esto es: si el producto es mayor que 9 se vuelven a meter todas las bolas en el bombo y se vuelve a empezar hasta que el producto sea un numero de una sola cifra).

2- Que solo sea válido cuando el resultado del producto sea un número de dos cifras. ( lo mismo que en la alternativa anterior pero no siendo válido cuando el producto es un número de una sola cifra)

3- Dejarlo todo tal cual estaba planteado al principio.

¿Qué elige?

Total posibles resultados : 72. Pares:52. Impares:20. 72,22 %veces par

Un dígito total: 20. Pares: 12 Impares: 8. 60% veces par

Dos dígitos total: 52. Pares: 40. impares: 12. 76,92%veces par.

Lotería, π y ayuda.

Hace días, viendo los decimales de “e” y de “pi” me topé con esta herramienta para descubrir la posición decimal que ocupa (si la ocupa) un número cualquiera dentro de los 200.000.000 primeros decimales de pi.

Me llamó la atención lo cerca que quedaban diversos números de 5 cifras, por ejemplo el 00026 lo encontramos en el lugar 22.759.

Estaba próxima la Lotería de Navidad (para los que no son de España les diré que es un gran acontecimiento que inaugura cada año las fiestas de Navidad) , por lo que jugué un rato a buscar el numero de 5 cifras que tarda más en aparecer en los decimales de pi. Por un momento me dije: “si lo encuentro seguro que es el que toca en la lotería”.

Después de muchos intentos encontré el 25.687, que no se encuentra hasta llegados al decimal 231.906 pero desistí de seguir buscando por mi falta de fe en esas premoniciones y porque necesitaría mucho tiempo probar los 85.000 números del sorteo de la Lotería de Navidad.

Hoy que se ha celebrado el tradicional sorteo me acordé de mi jueguecito y por curiosidad fui a ver que lugar ocupaba “el gordo”: el numero premiado, que ha sido el 78.294
y resulta que no aparece hasta el lugar:

578.987 ¡¡¡¡

¿será el último de 5 cifras en aparecer?

Necesito su ayuda para que encuentren urgentemente, usando la citada herramienta o como mejor sepan discurrir, otro número de 5 cifras entre el 00000 y el 84999, que ocupe un lugar posterior al decimal 578.687 dentro de los decimales de Pi.

Mientras tanto me estaré tirando de los pelos por no creer en las premoniciones y no haberlo buscado.

2 y 7 no cuadran con 26

Empleando solo sumas y restas del cuadrado de un máximo de 3 números distintos del 1 al 9 se puede obtener 26, de muchas formas:

Por ejemplo :

26 = 4² + 3²+ 1²
26 = 5² + 1²
26 = 6² - 3²- 1²
26 = 9² - 8² + 3²


Sin embargo si quiero emplear 7² o 2² para obtener 26 cumpliendo esa norma, no lo logro.

Se trata de encontrar un número en el que sí lo logramos. Esto es, que podamos emplear todos los cuadrados del 1 al 9 para obtenerlo en distintas formas que cumplan lo definido arriba.
Como reto añadido se valorará la que necesite el menor número de formas distintas para usar los 9 cuadrados.

El reino digital

En el tablero del reino de los números del 1 al 9,

- el 1 es el rey.

- Los números impares son los nobles y los pares los plebeyos,

- Las cuadrículas que estén en contacto con la del rey deben estar ocupadas por nobles, incluso si la tocan solo por la esquina.

- La fila en la que esta el rey, la columna a la que pertenece y una de las diagonales deben sumar lo mismo, la otra diagonal no puede sumar más que la anterior.

- Dos números consecutivos solo pueden tocarse entre si por sus esquinas

- Un único plebeyo puede estar en una fila superior a una ocupada por un noble, pero siempre a la izquierda de los nobles de su fila.


Coloque los números del reino en el tablero de la imagen siguiendo las leyes del reino.

¿Como saber si su distribución es la correcta?:

1º -Debe ser usted mayor de 18 años.

2º-Copie y pegue en su navegador la dirección que aparece a continuación sustituyendo previamente los asteriscos por los números en el orden de su solución (de izquierda y derecha y de arriba a abajo) después añada una A , si salen las SEIS MODELOS MÁS TOP EN PELOTAS su respuesta es correcta.

Si sus gustos son otros y prefiere verificar su solución viendo a VEINTISÉIS DESNUDO añada una B a los números de su solución, pero advierto que esta opción les puede causar algún tipo de trauma irreparable hasta el punto de que lamentará haber acertado.

http://blogs.ya.com/veintiseis/files/**********.jpg

NOTA IMPORTANTE.:
A los acertantes se les solicita encarecidamente eviten hacer comentarios soeces sobre lo visto en sus verificaciones.

Pares y nones

Siguiendo con los problemillas de la categoria que hemos llamado del 1 al 9 Hoy buscamos conseguir una igualdad con el mínimo de operadores matematicos básicos( +, -, x y /) que tenga los números pares (2, 4, 6 y 8) a un lado de la igualdad y los impares (1, 3, 5, 7 y 9) al otro.

Por ejemplo: 42+8-6=79-35x1 => 44=44 aquí hemos usado 4 operadores

¿lo puedes lograr con menos?

Del 1 al 9 por parentesco

Estirando un poco el modelo de problema visto recientemente; les propongo hoy, que utilizando una sola vez los números del 1 al 9, con los primos (1, 2, 3, 5 y 7) a la izquierda y el resto a la derecha forme una igualdad usando en menor número de operaciones matemáticas básicas (suma, resta, multiplicación y división).

Por ejemplo (con 4 operaciones):

35-12-7=96/8+4

¿alguien encuentra una con 3?, ¿o con 2?, ¿la habrá con 1?

Cuadrados que dan un primo

Sabiendo que todos los miembros del lado izquierdo de esta igualdad son cuadrados perfectos, sustituya las letras por los números del 1 al 9 y en los cuadraditos sitúe las operaciones matemáticas básicas oportunas para que se cumpla la igualdad :

¿Se podrá llegar a uno, exactamente a uno?

Intercale como máximo 4 cualquiera de los signos matemáticos básicos (suma ,resta, multiplicación y división) entre las cifras 123456789 así ordenadas, para obtener el resultado más próximo a 1.

Ejemplos:
12345/6789= 1,81

(12x345/67/8)-9=1,28

Paréntesis se pueden usar los que se estimen oportunos.